My findings from the study arose from my taking a closer look at the units of analysis. Transcribing and coding each Episode allowed me to perform a more detailed consideration of how the characteristics of an Episode of shared epistemic agency manifest in the classroom. I elaborated on the Episode and on how participants interact as they direct their agency towards the characteristics of shared epistemic agency. This elaboration help answer the research questions.
Recognising an Intention to resolve an unknowing.
An intention is the start of participants’ epistemic interaction that leads to the production of new knowledge. Hence it is essential to recognise it. Four features of an Intention are; orientation, who initiates it, its visibility and what triggers it.
- Orientation – An Intention can be expresses as an:
- Extension, a participant seeking to extend existing knowledge
- Explication, seeking to explicate knowledge to another participant
- Expertise, when a participants seeks to control the learning culture
- Initiated by – An Intention can be initiated by:
- A student participant
- A teacher participant
- Visibility – An intention can be made visible by:
- A dialogical interaction
- A physical interaction
- A reification, such as a tick in an exercise book. Reification is“the process of giving form to our experiences by producing objects that congeal this experience into ‘thingness’” (Wenger 1998 p. 58).
- Trigger – An intention can be triggered by:
- An identified unknowing – A participant identified their own unknowing and seeks a resolution.
- An assumed unknowing – A participant assumes the existence of unknown mathematics amongst other participants.
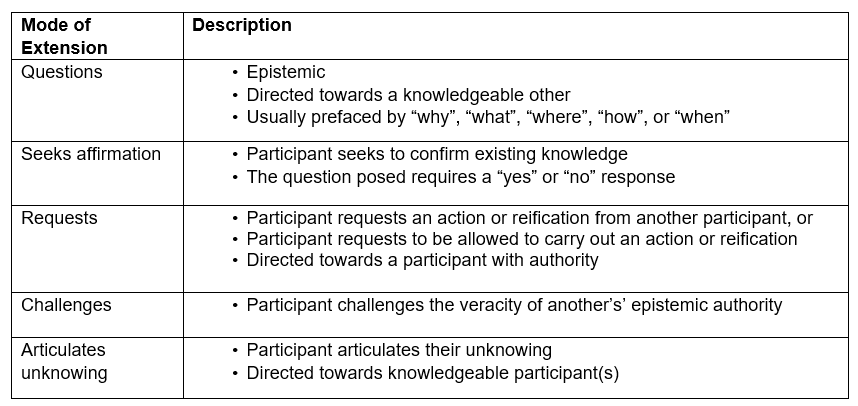
Recognising a mode of Extension in the classroom.
The modes of Extension demonstrate how participants sought to extend their mathematics knowledge in my mathematics classroom. I have summarised the five modes in the table below.
Recognising a mode of Explication in the classroom
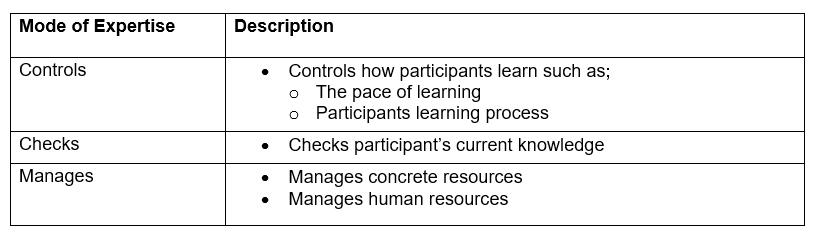
The modes of Explication demonstrate how the participants of my classroom made their mathematics knowledge explicit to other participants. I have summarised the four modes in the table below.

Recognising a modes of Expertise in the classroom
The modes of Expertise, by which participants directed their agency towards expressing process authority in the classroom community. I have summarised the three modes in the table below
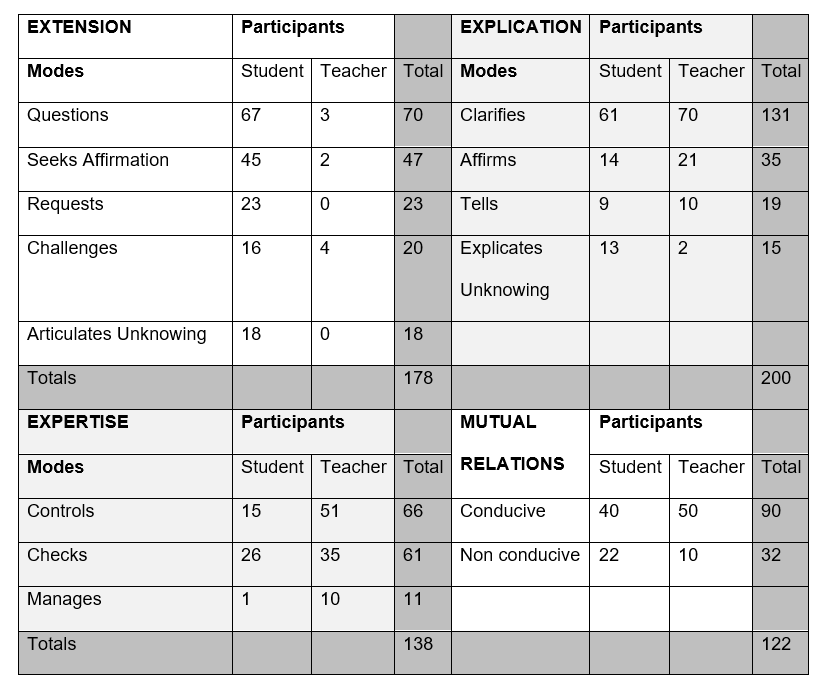
Mutual Relations is the characteristic of shared epistemic agency that highlights the ways participants channel their agency towards relating with other participants in the classroom community
I termed Mutual Relations conducive when the corresponding actions and reifications contribute to the advancement of mathematics knowledge, and non-conducive when they do not contribute to the advancement of mathematics knowledge.
The table below shows the number of times the different modes occurred across the 36 Episodes.
The resolution of an unknowing as New Knowledge
New mathematics knowledge emerges from knowledge building as a resolution of the unknowing that triggered the Intention. Given that it resolves an unknowing, this knowledge is new to the participants involved in the Episode, and is considered legitimate if it is able to resolve the unknowing for all participants involved in the Episode
It is not the emergence of the New Knowledge that brings the episode to an end. It is the participants acknowledging that the New Knowledge has resolved an unknowing that brings an Episode to a close. The end of an Episode occurs when participants no longer direct their agency towards further Extension. That is, when they no longer seek to extend their mathematics knowledge.
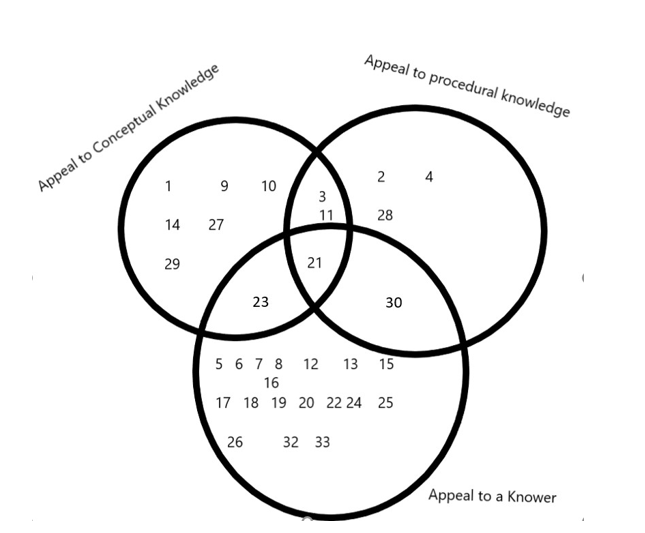
The students built new mathematics knowledge by appealing to procedural knowledge, a knowledgeable participant, conceptual understanding, or by combining two or all three of these appeals. The image below shows how participants built new knowledge across Episodes.
What was unique about participant’s interactions
I was particularly interested in participant epistemic interactions. The interactions highlighted what was unique about my classroom. This was an indicator of how the research met the study’s aims. I focused on three features of the pedagogy:
- Participants’ positioning during the interaction,
- How to process authority manifested in the classroom, and
- How participants’ epistemic authority impacted how they advanced mathematics knowledge in the classroom.
Positioning
- As students interact to advance their mathematics knowledge, they can be positioned flexibly as a learner, knower, or facilitator from moment to moment.
- The students can reflexively position themselves as a learner, knower, or facilitator; they can be interactionally positioned by others as a knower or facilitator; and can be institutionally positioned by the pedagogy as a facilitator.
Process authority
- Process authority emerges during epistemic interaction, and constitutes a blending of authority. This blending of authority arises from the mutual interdependency of the experiences and skills of the students and the teacher. Students controlled their dialogical and physical actions in the learning environment during epistemic interaction
- The student is an authority, and can influence the behaviour of other participants when in the learner position. The student is also knowledgeable in this position.
Epistemic authority
- Participation in a learning community is democratic and proceeds without regard for the school’s ability labels ascribed to students. Students enacted the pedagogy irrespective of the ability labels assigned to them by the school, and they took responsibility for their individual and collective knowledge advancement.